GDG on Campus: PTIT - Probation Contest #2
The Animatronic
SubmitPoint: 1
Problem
đang chuẩn bị cho ca làm việc đêm tại nhà hàng Freddy Fazbear's Pizzeria. Để theo dõi sát sao tất cả các Animatronic, anh ấy cần mua số lượng lớn các camera để lắp và theo dõi chúng.
được nhà hàng cấp cho ~K~ đơn vị tiền tệ. Trước ca đêm của mình, anh ấy sẽ đi tới cửa hàng bán camera để mua, cửa hàng có ~N~ loại camera, mỗi loại camera có giá ~C_i~ đơn vị tiền tệ. Để theo dõi được hết tất cả các Animatronic, anh ấy cần mua càng nhiều camera càng tốt. Bạn hãy giúp anh ấy tìm ra anh ấy có thể mua được tối đa bao nhiêu camera với ~K~ đơn vị tiền tệ?
Input
Dòng đầu tiên chứa một số nguyên dương ~N~ ~(1 \leq N \leq 10^4)~.
Dòng thứ hai chứa một số nguyên ~K~ ~(1 \leq K \leq 10^{18})~
~N~ dòng tiếp theo, mỗi dòng chứa một số nguyên dương ~C_i~ ~(0 \leq C_i \leq 10^{18})~ sao cho ~(1 \leq i \leq N)~.
Output
In ra một dòng chứa một số nguyên dương duy nhất là số lượng camera tối đa mà có thể mua.
Sample
| Sample Input | Sample Output |
|---|---|
|
5
500
500
80
100
230
70
|
4
|
Giải thích
Để mua được nhiều camera nhất sẽ mua các camera có giá trị là ~80, 100, 230, 70~ có tổng là ~480 \leq 500~. Nên đáp án là 4.
Magic Gate
SubmitPoint: 1
Problem
Trong thành phố Cơ Số, mỗi cổng dịch chuyển chỉ mở khi bạn trả đúng tổ hợp bùa. Có hai loại bùa:
- Bùa loại ~A~ (mỗi lá trị giá ~a~ đơn vị năng lượng),
- Bùa loại ~B~ (mỗi lá trị giá ~b~ đơn vị năng lượng).
Để mở cổng lớn dẫn vào Thư Khố, bạn cần đúng ~n~ đơn vị năng lượng. Người gác cổng cho phép bạn chọn hai túi bùa với số lượng không âm: túi thứ nhất chứa ~x~ lá bùa loại ~A~, túi thứ hai chứa ~y~ lá bùa loại ~B~. Cổng sẽ mở nếu và chỉ nếu tổng năng lượng đạt được chính xác đạt yêu cầu, trong đó ~x, y~ là số nguyên không âm (có thể bằng 0).
Hãy xác định xem có cách chọn ~x~ và ~y~ để mở cổng hay không.
Input
Ba dòng chứa ba số nguyên dương ~a, b, n~.
Output
In ra YES nếu cổng có thể mở được, nếu bất khả thi in ra NO.
Constraints
~1 \le a, b, n \le 10^{18}~.
Sample
| Sample Input | Sample Output |
|---|---|
|
7
10
16
|
NO
|
|
7
10
70
|
YES
|
The Cenobite
SubmitPoint: 1
Problem
Trong một chiều không gian khác, The Cenobite, một thực thể của trật tự và hỗn mang, đã tạo ra một câu đố mới. Hắn đưa cho bạn một khối cấu hình (Lament Configuration) dưới dạng một dãy ~N~ khối năng lượng. Một khối có một mức năng lượng là một số nguyên.
Trạng thái cân bằng của Khối Cấu Hình đạt được khi sự chênh lệch năng lượng giữa hai khối bất kỳ liền kề nhau không vượt quá một ngưỡng ~T~ cho trước.
The Cenobite thực hiện một nghi lễ gọi là Sự Hài Hòa. Trong mỗi lượt của nghi lễ, hắn sẽ quét qua Khối Lament từ trái sang phải (từ vị trí ~0~ đến ~N-2~). Đối với mỗi cặp khối liền kề ~A_i~ và ~A_{i+1}~, nếu chúng bất cân bằng -- tức chênh lệch năng lượng lớn hơn ~T~, hắn sẽ ngay lập tức điều chỉnh năng lượng của khối ~A_{i+1}~. để nó trở nên cân bằng với ~A_i~. Cụ thể:
- Nếu ~A_{i+1} > A_i + T~, thì năng lượng của ~A_{i+1}~ sẽ được giảm xuống ~T~ năng lượng.
- Nếu ~A_{i+1} < A_{i} -T~, thì năng lượng của ~A_{i+1}~ sẽ được tăng lên ~T~ năng lượng.
Nghi lễ này sẽ lặp đi lặp lại cho đễn khi toàn bộ khối Lament đạt đến Trạng thái Cân Bằng, tức là sau một lượt quét hoàn chỉnh mà không có khối nào cần phải điều chỉnh (mỗi lượt quét kể cả không có sự thay đổi vẫn được tính).
Nhiệm vụ của bạn khi đối mặt với The Cenobite là cần thực hiên bao nhiêu lượt trong nghi lễ Sự Hài Hòa để đưa khối Lament về trạng thái cân bằng.
Input
Dòng đầu tiên chứa một số nguyên dương ~N~ ~(2 \leq N \leq 1000).~
Dòng thứ hai chứa một số nguyên dương ~T~ ~(0 \leq T \leq 10^5)~.
~N~ dòng tiếp theo mỗi dòng chứa một số nguyên ~A_i~ ~(-10^5 \leq A_i \leq 10^5)~.
Output
In ra một số nguyên duy nhất là số lượt cần thiết trong nghi lễ để khối Lament về trạng thái cân bằng.
Sample
| Sample Input | Sample Output |
|---|---|
|
5
10
10
50
20
70
30
|
4
|
Thần thú
SubmitPoint: 1
Problem
Trong thời đại thần thoại Ánh Sương, vương quốc Eldoria muốn rước Thánh Hỏa từ Đền Bình Minh về Kinh Đô để làm lễ đăng quang. Nhiệm vụ được giao cho đoàn kỵ sĩ hộ tống do tướng trẻ Arion dẫn đầu. Arion phải chọn một trong số nhiều thần thú đang ràng buộc ở Chuồng Thiêng: mỗi thần thú có giá chuộc khác nhau và một bầu linh lực có thể tích trữ tối đa một lượng năng lượng nhất định.
Con đường từ Kinh Đô đến Đền Bình Minh là một tuyến thẳng dài ~d~ dặm. Trên đường có đặt q miếu tế (điểm an trú), tại mỗi miếu bầu linh lực sẽ được nạp đầy ngay khi đoàn tới nơi. Mỗi thần thú có thể di chuyển với hai nhịp:
- Nhịp thường: tốc độ 1 dặm/đơn vị thời gian, tiêu hao 1 đơn vị linh lực cho mỗi dặm đã đi.
- Nhịp thần tốc: tốc độ 2 dặm/đơn vị thời gian, tiêu hao 2 đơn vị linh lực cho mỗi dặm đã đi.
Trong từng quãng đường giữa hai điểm dừng liên tiếp (Kinh Đô → miếu 1, miếu 1 → miếu 2, …, miếu q → Đền), Arion có thể tùy ý thay đổi nhịp di chuyển, miễn là tổng linh lực tiêu thụ trên quãng ấy không vượt quá sức chứa của bầu linh lực của thần thú đã chọn. Nghi lễ bắt đầu sau đúng ~t~ đơn vị thời gian kể từ lúc rời Kinh Đô; nếu đến muộn, Thánh Hỏa sẽ tắt.
Hãy giúp Arion chọn một thần thú sao cho:
1) Có thể đi trọn hành trình mà không cạn linh lực giữa đường (nhờ nạp đầy tại các miếu),
2) Thời gian ngắn nhất có thể đạt được với thần thú đó không vượt quá ~t~,
3) Giá chuộc là nhỏ nhất trong số các thần thú thỏa hai điều kiện trên.
Nếu có thần thú phù hợp, hãy in giá chuộc nhỏ nhất; nếu không, in No hope!.
Input
- Dòng 1: bốn số nguyên ~n, q, d, t~ — số thần thú, số miếu tế, chiều dài đường và hạn thời gian.
- ~n~ dòng tiếp theo: dòng thứ ~i~ chứa hai số nguyên ~v[i], f[i]~ — giá chuộc và sức chứa linh lực của thần thú thứ ~i~.
- ~q~ dòng tiếp theo: mỗi dòng chứa số nguyên ~a[j]~ — vị trí miếu thứ ~j~ tính từ Kinh Đô (đơn vị dặm).
Output
In ra giá chuộc nhỏ nhất của một thần thú thỏa yêu cầu. Nếu không có, in No hope!.
Constraints
- ~1 \le n, q \le 10^5~
- ~1 \le d \le 2 \cdot 10^9~
- ~1 \le t \le 10^{9}~
- ~1 \le v[i], f[i] \le 10^{9}~
- ~1 \le a[j] \le d-1~ và các ~a[j]~ đôi một khác nhau.
Sample
| # | Input | Output |
|---|---|---|
| 1 |
4 2 7 15
10 9
4 4
9 3
4 10
1
6
|
4
|
The Elysium
SubmitPoint: 1
Problem
Tại Elysium, một vùng đất thần thoại, các nhà tiên tri theo dõi dòng chảy năng lượng của vũ trụ. Dòng chảy này được biểu diễn dưới dạng một chuỗi các giá trị số nguyên. Để khám phá những bí mật sâu xa nhất, họ cần xác định khoảng thời gian mà năng lượng vũ trụ đạt đến đỉnh điểm. Họ sử dụng một kỹ thuật cổ xưa gọi là Thấu Kính Thời Gian để phân tích các đoạn năng lượng liên tiếp.
Có ~N~ dòng chảy năng lượng vũ trụ mỗi dòng chảy có năng lương là ~A_i~. đặt một số ~K~ là độ rộng của Thấu Kính Thời Gian. Nhiệm vụ của bạn là tìm ra các dòng chảy năng lượng vũ trụ liên tiếp có độ dài là ~K~ để thấu kính có thể nhìn thấy hết ~K~ dòng chảy năng lượng này, sao cho tổng năng lượng của các dòng chảy là lớn nhất.
Input
Dòng đầu tiên chứa hai số nguyên ~N~ ~(1 \leq N \leq 10^5)~.
Dòng thứ hai chứa một số nguyên ~K~ ~(1 \leq K \leq N \leq 10^5)~.
~N~ dòng tiếp theo mỗi dòng chứa một số nguyên ~A_i~ là năng lượng của dòng chảy thứ ~i~ ~(-1000 \leq A_i \leq 1000)~.
Output
In ra một số nguyên duy nhất là tổng năng lượng lớn nhất tìm được trong một dãy các dòng chảy năng lượng liên tiếp có độ dài là ~K~.
Sample
| Sample Input | Sample Output |
|---|---|
|
8
3
1
4
2
10
2
3
1
5
|
16
|
Giải thích
Dòng chảy năng lượng ~A~ có ~8~ giá trị và độ rộng thấu kính ~K~ là ~3~. Chúng ta cần xem xét tất cả các dãy năng lượng liên tiếp có độ dài là ~3~.
Ta dễ thấy dãy ~[4, 2, 10]~ có tổng năng lượng là ~16~. Do đó, kết quả là ~16~.
Stairs
SubmitPoint: 1
Problem
Trên đỉnh Thư Khố có hai bậc thang song sinh dẫn tới Cổng Thời Gian. Mỗi mùa thi, học viên nhận một con số linh ấn ~n~ và phải đánh thức cả hai bậc thang bằng cách rải những viên ấn khắc số.
Bậc thang bên trái là bậc thang đi xuống: từ sân thượng, những viên ấn mang số lớn dần như dòng cát chảy ngược, đổ xuống từng bậc mỗi lần ít đi một viên cho tới khi chỉ còn lại tiếng kim rơi. Bậc thang bên phải lại đi lên: khởi đầu từ một con số bé nhỏ nơi mặt đất, mỗi bậc thêm một viên, từng dấu khắc lớn dần như nhịp tim của đá.
Khi nghi thức hoàn tất, toàn bộ các con số khắc trên hai bậc thang — từ viên đầu tiên đặt xuống cho tới viên cuối cùng chạm đích — kết nối với nhau thành một câu chuyện khép kín: câu chuyện bắt đầu ở đỉnh và kết lại tại chân, nhưng nếu bạn lần theo vết khắc, bạn sẽ biết phải đặt từng con số ở đâu.
Bạn chỉ được trao ~n~. Hãy hoàn thành nghi thức.
Input
Một dòng duy nhất chứa số nguyên dương ~n~.
Output
In ra hai khối:
- Khối thứ nhất là bậc thang đi xuống (mỗi dòng cách nhau bởi dấu xuống dòng, các số trên một dòng cách nhau bởi một khoảng trắng).
- Sau đó đến khối thứ hai là bậc thang đi lên với định dạng tương tự.
Constraints
~1 \le n \le 1000~.
Sample
| Sample Input | Sample Output |
|---|---|
|
5
|
15 14 13 12 11
10 9 8 7
6 5 4
3 2
1
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
|
Infinity
SubmitPoint: 1
Problem
Để cho bài toán được đơn giản, chúng ta hãy giả định rằng biểu tượng Vô cực được tạo thành từ những hình tròn tiếp xúc ngoài tại điểm ~S~ như được minh họa bên dưới, và chúng ta sẽ gọi đó là tâm của vô cực.
Bạn được cho ba số nguyên ~R~, ~A~, ~B~. Bạn hiện đang ở tại tâm của vô cực. Trước tiên, bạn sẽ bắt đầu vẽ hình tròn bên phải với bán kính ~R~ và sau đó quay trở lại tâm của vô cực. Kế tiếp, bạn bắt đầu vẽ hình tròn bên trái với bán kính bằng bán kính của hình tròn trước đó nhân với ~A~. Sau khi đến tâm của vô cực, bạn lại bắt đầu vẽ hình tròn bên phải với bán kính bằng bán kính của hình tròn trước đó chia cho ~B~. Sau khi đến tâm của vô cực, bạn lại vẽ hình tròn bên trái với bán kính bằng bán kính của hình tròn trước đó nhân với ~A~.
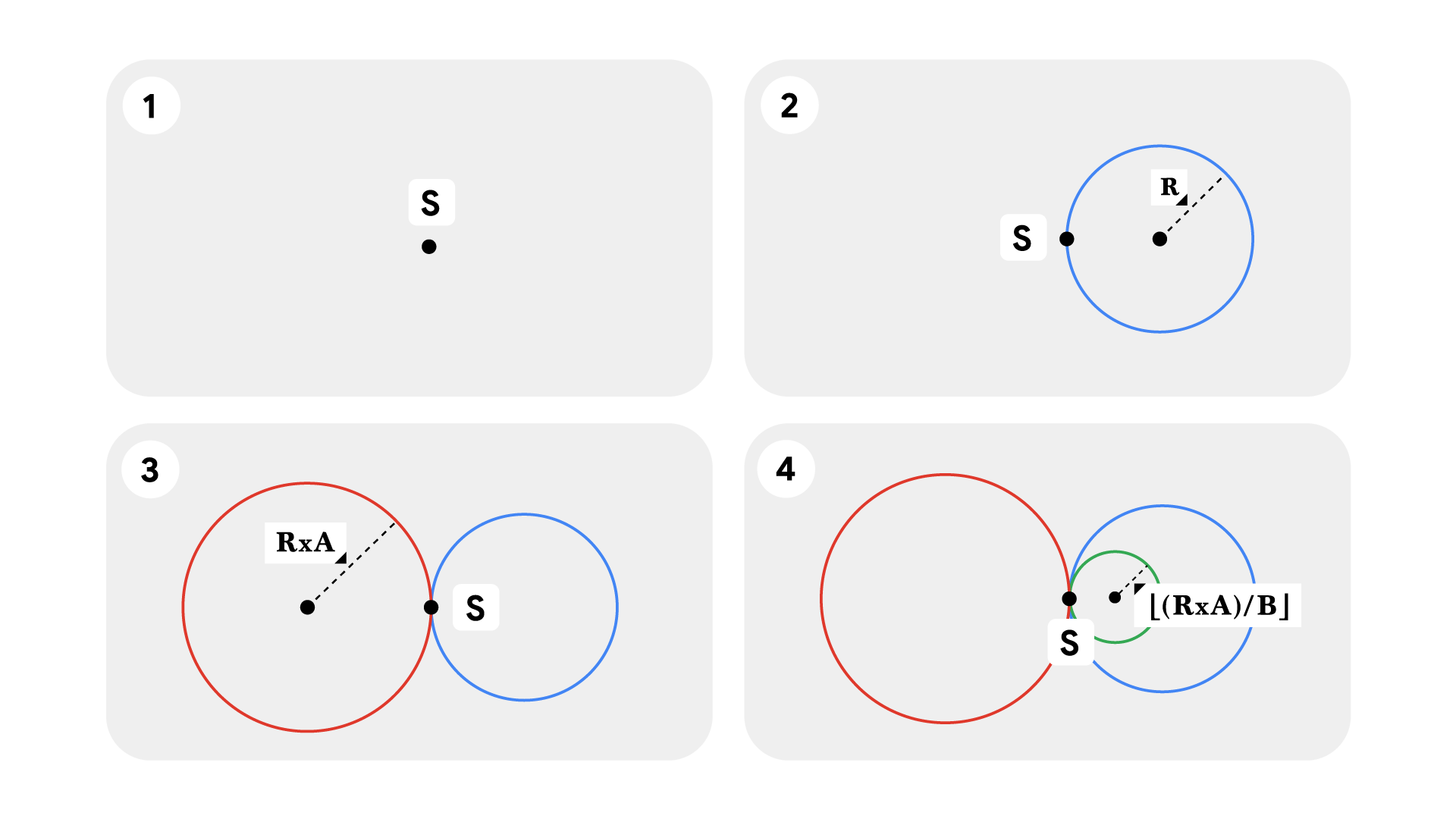
Bạn hãy tiếp tục vẽ các hình tròn bên trái và bên phải theo quy trình đã mô tả ở trên cho đến khi bán kính của hình tròn cần vẽ bằng không. Hãy tính tổng diện tích của tất cả các hình tròn đã được vẽ.
Bài toán đảm bảo rằng quy trình này sẽ dừng lại sau một số bước hữu hạn.
Input
Gồm 3 dòng lần lượt là các số nguyên ~R, A, B~ sao cho:
- ~1 \leq R \leq 10^5~.
- ~1 \leq A \leq 500~.
- ~2 \times A \leq B \leq 1000~.
Output
In ra một dòng chứa tổng diện tích của tất cả hình tròn được vẽ cho đến khi bán kính của hình tròn bằng ~0~.
Đáp án của bạn sẽ được chấp thuận nếu sai số tuyệt đối hoặc tương đối của bạn so với câu trả lời đúng nhỏ hơn ~10^{-6}~ (làm tròn đến ~6~ chữ số thập phân).
Sample
| Sample Input | Sample Output |
|---|---|
|
1
3
6
|
31.415927
|
|
5
2
5
|
455.530935
|
Giải thích
Trong ví dụ đầu tiên, bạn bắt đầu bằng cách vẽ hình tròn bên phải có bán kính ~1~ đơn vị. Sau khi đạt đến tâm vô cực, bạn vẽ hình tròn bên trái có bán kính ~1 \times 3 = 3~ đơn vị. Sau khi đạt đến tâm vô cực, bạn dừng vẽ hình tròn bên phải vì bán kính trở thành ~\lfloor 3/6 \rfloor = 0~ đơn vị. Do đó, tổng diện tích của các hình tròn được vẽ là ~\pi \times 1^2 + \pi \times 3^2 \approx 31,415927~.
Trong trường hợp ví dụ thứ hai, bạn bắt đầu bằng cách vẽ hình tròn bên phải với bán kính ~5~ đơn vị. Sau khi đạt đến tâm vô cực, bạn vẽ hình tròn bên trái với bán kính ~5 \times 2 = 10~ đơn vị. Sau khi đạt đến tâm vô cực, bạn vẽ hình tròn bên phải với bán kính ~\lfloor 10/5 \rfloor = 2~ đơn vị. Sau khi đạt đến tâm vô cực, bạn vẽ hình tròn bên trái với bán kính ~2 \times 2 = 4~ đơn vị. Sau khi đạt đến tâm vô cực, bạn dừng vẽ vì bán kính của hình tròn tiếp theo trở thành ~\lfloor 4/5 \rfloor = 0~ đơn vị. Do đó, tổng diện tích của các hình tròn đã vẽ là ~\pi \times 5^2 + \pi \times 10^2 + \pi \times 2^2 + \pi \times 4^2 ≈ 455,530935~.
Deliverence
SubmitPoint: 1
Problem
Một robot giao hàng được giao nhiệm vụ phân phát các gói hàng dọc theo một con đường thẳng dài ~N~ mét, bắt đầu từ điểm ~0~. Robot này có một đặc tính lạ: nó chỉ có thể dừng lại và giao hàng tại các điểm có khoảng cách là bội số của ~K~ (ví dụ: ~K, 2 \times K, 3 \times K, \dots~). Robot sẽ phải giao một gói hàng tại tất cả các điểm dừng hợp lệ trên quãng đường từ ~1~ đến ~N~.
Hãy tính tổng khoảng cách của tất cả các điểm mà robot đã dừng lại để giao hàng.
Input
Dòng đầu tiên chứa một số nguyên dương ~N~ ~(1 \leq N \leq 10^6)~.
Dòng thứ hai chứa một số nguyên ~K~ ~(1 \leq K \leq 10^6)~
Output
In ra một dòng chứa một số nguyên duy nhất là kết quả của bài toán.
Sample
| Sample Input | Sample Output |
|---|---|
|
20
5
|
50
|
|
10
3
|
18
|
|
7
8
|
0
|
Giải thích
Với ~N = 20~ và ~K = 5~, robot sẽ dừng tại các điểm ~5, 10, 15, 20~. Tổng khoảng cách là ~5 + 10 + 15 + 20 = 50~.
Back to the basic
SubmitPoint: 1
Problem
Cho 4 số nguyên dương ~A, B, C~ và ~D~. Liệu có tồn tại một số nguyên dương ~N~ sao cho:
- ~N~ xuất hiện trong khoảng từ ~A~ đến ~B~ (bao gồm cả ~A~ và ~B~).
- ~N~ xuất hiện trong khoảng từ ~C~ đến ~D~ (bao gồm cả ~C~ và ~D~).
Input
Gồm ~4~ dòng lần lượt là các số nguyên dương ~A, B, C~ và ~D~ ~(1 \leq A, B, C, D \leq 10^{18})~.
Output
Nếu có ít nhất 1 số nguyên dương ~N~ thỏa mãn điều kiện, in ra YES, ngược lại in ra NO.
Sample
| Sample Input | Sample Output |
|---|---|
|
1
3
2
4
|
YES
|
|
1
2
3
4
|
NO
|
Thanh tẩy thẻ bài
SubmitPoint: 1
Problem
Hệ Thống Thẻ Bài của Vương quốc Số bị nhiễu loạn: mỗi thẻ là một số nguyên không âm rất lớn. Để thanh tẩy một thẻ, pháp sư phải liên tục gom năng lượng chữ số của nó: cộng tất cả các chữ số lại với nhau, rồi thay thẻ bằng tổng vừa nhận được, và lặp lại cho đến khi thẻ chỉ còn một chữ số.
Ví dụ, một thẻ ghi ~278~ sẽ được thanh tẩy theo chuỗi ~278 \rightarrow 17 \rightarrow 8~, nên khi thanh tẩy xong ta sẽ nhận được thẻ là ~8~.
Nhiệm vụ của bạn là giúp pháp sư thanh tẩy một thẻ bài có số nguyên không âm ~N~.
Input
Gồm 1 dòng chứa số nguyên không âm ~N~.
Output
In ra một chữ số là dạng rút gọn của ~N~.
Constraints
~0 \le N \le 10^{18}~.
Sample
| Sample Input | Sample Output |
|---|---|
|
999991020
|
3
|
|
0
|
0
|
Lại là hình tròn
SubmitPoint: 1
Problem
Bạn được giao hai vòng tròn trên mặt phẳng. Hãy tính diện tích phần giao nhau của chúng.
Input
Dòng đầu chứa ba số nguyên ~x_1, y_1, r_1~ ~(-10^9 \le x_1, y_1 \le 10^9,\ 1 \le r_1 \le 10^9)~ — tọa độ tâm và bán kính của vòng tròn thứ nhất.
Dòng tiếp theo chứa ba số nguyên ~x_2, y_2, r_2~ ~(-10^9 \le x_2, y_2 \le 10^9,\ 1 \le r_2 \le 10^9)~ — tọa độ tâm và bán kính của vòng tròn thứ hai.
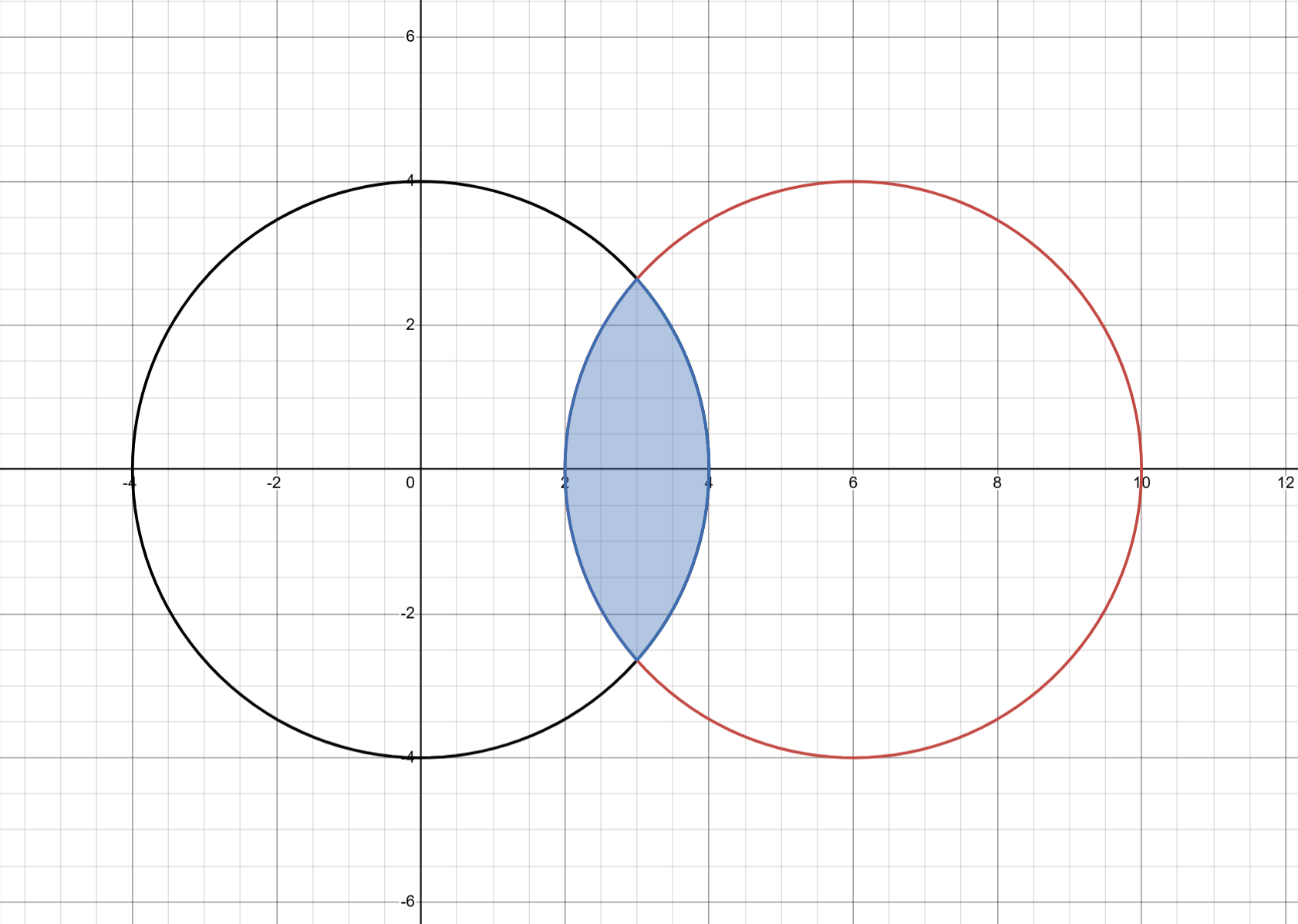
Output
In ra diện tích phần giao nhau của hai vòng tròn. Kết quả được chấp nhận nếu sai số tuyệt đối hoặc tương đối không vượt quá ~10^{-6}~.
Chú ý: Dùng code sau để nhập dữ liệu
x1, y1, r1 = map(int, input().split())
x2, y2, r2 = map(int, input().split())
Sample
| Sample Input | Sample Output |
|---|---|
|
0 0 4
6 0 4
|
7.25298806364175601379
|
|
0 0 5
11 0 5
|
0.00000000000000000000
|
Cột trụ trời
SubmitPoint: 1
Problem
Trong Thánh Địa Chronia có hai Cột Trụ Dao Động dùng để tích lũy mảnh thời tinh.
- Cột Trụ Alpha: mỗi ngày hoạt động tạo ra ~a~ mảnh. Do cộng hưởng quá tải, cứ đến các ngày ~x, 2x, 3x, \ldots~ thì Alpha tắt hoàn toàn trong cả ngày đó (không tạo mảnh).
- Cột Trụ Beta: mỗi ngày hoạt động tạo ra ~b~ mảnh và sẽ tắt vào các ngày ~y, 2y, 3y, \ldots~.
Thời gian bắt đầu từ ngày 1. Vào mỗi ngày, hai cột trụ cùng được kích hoạt; nếu trùng ngày tắt của cột nào thì cột đó không tạo mảnh trong ngày ấy.
Hội Đồng Thủ Hộ cần tích đủ ~n~ mảnh thời tinh để khởi động Cổng Niên Kỷ. Hãy xác định ngày sớm nhất (tính từ ngày 1) để kích hoạt được Cổng Niên Kỷ.
Input
Một dòng với 5 số nguyên dương ~a, x, b, y, n~.
Output
Với mỗi bộ test, in ra số ngày nhỏ nhất cần thiết để đạt đủ ~n~ mảnh.
Constraints
- ~1 \le a, b, x, y, n \le 10^9~
- Dữ liệu đảm bảo không có trường hợp ~x = y = 1~.
Chú ý: Dùng code sau để nhập dữ liệu
a, x, b, y, n = map(int, input().split())
Sample
| # | Input | Output |
|---|---|---|
|
1
|
2 3 2 3 25
|
10
|