Attempt

Please login to see your submissions result.

Problem

Để cho bài toán được đơn giản, chúng ta hãy giả định rằng biểu tượng Vô cực được tạo thành từ những hình tròn tiếp xúc ngoài tại điểm ~S~ như được minh họa bên dưới, và chúng ta sẽ gọi đó là tâm của vô cực.

Bạn được cho ba số nguyên ~R~, ~A~, ~B~. Bạn hiện đang ở tại tâm của vô cực. Trước tiên, bạn sẽ bắt đầu vẽ hình tròn bên phải với bán kính ~R~ và sau đó quay trở lại tâm của vô cực. Kế tiếp, bạn bắt đầu vẽ hình tròn bên trái với bán kính bằng bán kính của hình tròn trước đó nhân với ~A~. Sau khi đến tâm của vô cực, bạn lại bắt đầu vẽ hình tròn bên phải với bán kính bằng bán kính của hình tròn trước đó chia cho ~B~. Sau khi đến tâm của vô cực, bạn lại vẽ hình tròn bên trái với bán kính bằng bán kính của hình tròn trước đó nhân với ~A~.

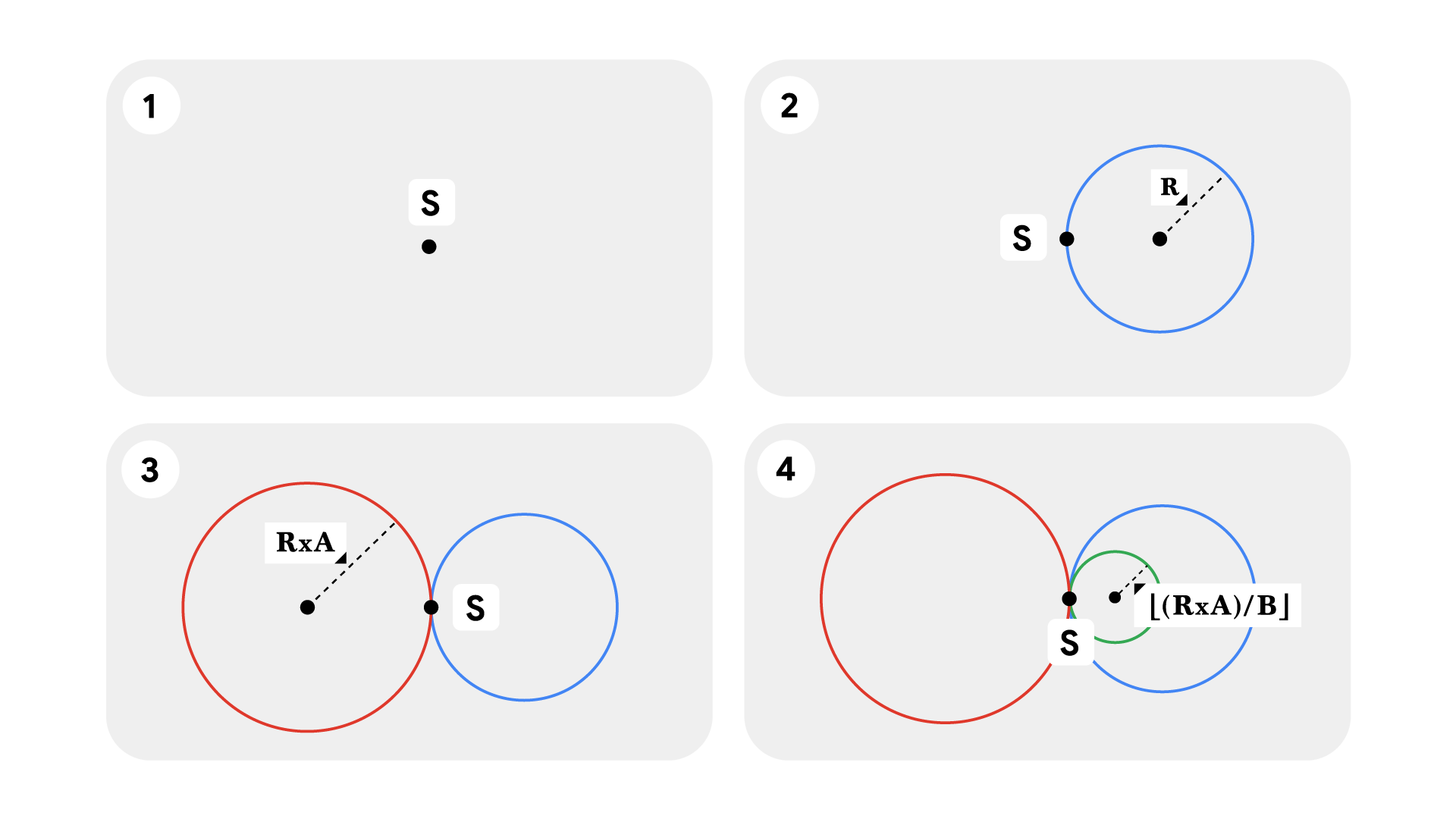
Bạn hãy tiếp tục vẽ các hình tròn bên trái và bên phải theo quy trình đã mô tả ở trên cho đến khi bán kính của hình tròn cần vẽ bằng không. Hãy tính tổng diện tích của tất cả các hình tròn đã được vẽ.

Bài toán đảm bảo rằng quy trình này sẽ dừng lại sau một số bước hữu hạn.

Input

Gồm 3 dòng lần lượt là các số nguyên ~R, A, B~ sao cho:

• ~1 \leq R \leq 10^5~.
• ~1 \leq A \leq 500~.
• ~2 \times A \leq B \leq 1000~.

Output

In ra một dòng chứa tổng diện tích của tất cả hình tròn được vẽ cho đến khi bán kính của hình tròn bằng ~0~.

Đáp án của bạn sẽ được chấp thuận nếu sai số tuyệt đối hoặc tương đối của bạn so với câu trả lời đúng nhỏ hơn ~10^{-6}~ (làm tròn đến ~6~ chữ số thập phân).

Sample

Giải thích

Trong ví dụ đầu tiên, bạn bắt đầu bằng cách vẽ hình tròn bên phải có bán kính ~1~ đơn vị. Sau khi đạt đến tâm vô cực, bạn vẽ hình tròn bên trái có bán kính ~1 \times 3 = 3~ đơn vị. Sau khi đạt đến tâm vô cực, bạn dừng vẽ hình tròn bên phải vì bán kính trở thành ~\lfloor 3/6 \rfloor = 0~ đơn vị. Do đó, tổng diện tích của các hình tròn được vẽ là ~\pi \times 1^2 + \pi \times 3^2 \approx 31,415927~.

Trong trường hợp ví dụ thứ hai, bạn bắt đầu bằng cách vẽ hình tròn bên phải với bán kính ~5~ đơn vị. Sau khi đạt đến tâm vô cực, bạn vẽ hình tròn bên trái với bán kính ~5 \times 2 = 10~ đơn vị. Sau khi đạt đến tâm vô cực, bạn vẽ hình tròn bên phải với bán kính ~\lfloor 10/5 \rfloor = 2~ đơn vị. Sau khi đạt đến tâm vô cực, bạn vẽ hình tròn bên trái với bán kính ~2 \times 2 = 4~ đơn vị. Sau khi đạt đến tâm vô cực, bạn dừng vẽ vì bán kính của hình tròn tiếp theo trở thành ~\lfloor 4/5 \rfloor = 0~ đơn vị. Do đó, tổng diện tích của các hình tròn đã vẽ là ~\pi \times 5^2 + \pi \times 10^2 + \pi \times 2^2 + \pi \times 4^2 ≈ 455,530935~.